Van der Waerden's theorem states that for any positive integers r and k there exists a positive integer N such that if the integers {1, 2, ..., N} are colored, each with one of r different colors, then there are at least k integers in arithmetic progression all of the same color. The smallest such N is the van der Waerden number W(r, k).
As follow up from the article
Heuristic lumped Stirling of mathematics, cardinality, induction, and the axiom of choice at Hilbert's paradox of the Grand Hotel
Combat Naps - Success Early On
Three Laws, Four Basic Forces and Four types of bonds
Van der Waerden test: Named after the Dutch mathematician Bartel Leendert van der
Waerden, the Van der Waerden test is a statistical test that k
population distribution functions are equal. The Van der Waerden test
converts the ranks from a standard Kruskal-Wallis one-way analysis of variance to quantiles of the standard normal distribution (details
given below). These are called normal scores and the test is computed
from these normal scores.
The k population
version of the test is an extension of the test for two populations
published by Van der Waerden (1952,1953).
VAN LINT–MACWILLIAMS’ CONJECTURE AND MAXIMUM CLIQUES IN
CAYLEY GRAPHS OVER FINITE FIELDS
SHAMIL ASGARLI AND CHI HOI YIP
Analysis of Variance (ANOVA) is a data analysis technique for examining the significance of the factors (independent variables) in a multi-factor model. The one factor model can be thought of as a generalization of the two sample t-test. That is, the two sample t-test is a test of the hypothesis that two population means are equal. The one factor ANOVA tests the hypothesis that k population means are equal. The standard ANOVA assumes that the errors (i.e., residuals) are normally distributed. If this normality assumption is not valid, an alternative is to use a non-parametric test.
The
letter alpha represents various concepts in physics and chemistry,
including alpha radiation, angular acceleration, alpha particles,
alpha carbon and strength of electromagnetic interaction (as
Fine-structure constant). Alpha also stands for thermal expansion
coefficient of a compound in physical chemistry. It is also commonly
used in mathematics in algebraic solutions representing quantities
such as angles. Furthermore, in mathematics, the letter alpha is used
to denote the area underneath a normal curve in statistics to denote
significance level when proving null and alternative hypotheses.
chasm K clique number v. schism clan complex network
Getting Beta to unity with Polywell polynomials: The beta function is the name used by Legendre and
Whittaker and Watson (1990) for the beta integral
(also called the Eulerian integral of the first kind). In mathematics, the beta function, is also called the Euler integral of the first kind.
Scaling laws of electron confinement and power losses in zero and low beta Polywell devices by David Vaughan Gummersall
In mathematics, the gamma function (represented by Γ, the capital Greek alphabet letter gamma) is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers.
A prime reciprocal magic square is a magic square using the decimal digits of the reciprocal of a prime number.
Scaling laws of electron confinement and power losses in zero and low beta Polywell devices by David Vaughan Gummersall
In mathematics, the gamma function (represented by Γ, the capital Greek alphabet letter gamma) is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers.
A prime reciprocal magic square is a magic square using the decimal digits of the reciprocal of a prime number.
Psychopomps (from the Greek word ψυχοπομπός, psuchopompos, literally meaning the "guide of souls") are creatures, spirits, angels, or deities in many religions whose responsibility is to escort newly deceased souls from Earth to the afterlife. Their role is not to judge the deceased, but simply to guide them. Appearing frequently on funerary art, psychopomps have been depicted at different times and in different cultures as anthropomorphic entities, horses, deer, dogs, whip-poor-wills, ravens, crows, owls, sparrows and cuckoos. When seen as birds, they are often seen in huge masses, waiting outside the home of the dying.
Tarakeshwara or Tarakeshvara (Sanskrit: तारकेश्वर, Tārakeśvara; Hindi: Tārkeśvar) is a form of the Hindu god Shiva in his role as a psychopomp, a ferryman or deliverer of the soul into freedom from rebirth (moksha). Taraka mantra, are various mantras spoken by Hindus at their deaths. As well, in a different religion, a Shiva is the week-long mourning period in Judaism for first-degree relatives.
Tarakeshwara or Tarakeshvara (Sanskrit: तारकेश्वर, Tārakeśvara; Hindi: Tārkeśvar) is a form of the Hindu god Shiva in his role as a psychopomp, a ferryman or deliverer of the soul into freedom from rebirth (moksha). Taraka mantra, are various mantras spoken by Hindus at their deaths. As well, in a different religion, a Shiva is the week-long mourning period in Judaism for first-degree relatives.
The Gamma and Beta Functions
Pi Day is an annual celebration of the mathematical constant π. Pi Day is observed on March 14 since 3, 1, and 4 are the first three significant digits of π.
A History of Pi (also titled A History of π) is a 1970 non-fiction book by Petr Beckmann that presents a layman's introduction to the concept of the mathematical constant pi (π).
"End of Life Doula", is another form of psychopomp work.
Palliative-pollution pundit Pruitt
In number theory, Waring's prime number conjecture is a conjecture related to Vinogradov's theorem, named after the English mathematician Edward Waring. It states that every odd number exceeding 3 is either a prime number or the sum of three prime numbers. It follows from the generalized Riemann hypothesis and (trivially) from Goldbach's weak conjecture.Van der Waals force
Van der Waals forces play a fundamental role in fields as diverse as secondary school science, supramolecular chemistry, structural biology, polymer science, nanotechnology, surface science, and condensed matter physics. Van der Waals forces also define many properties of organic compounds and molecular solids, including their solubility in polar and non-polar media.
If no other forces are present, the point at which the force becomes repulsive rather than attractive as two atoms near one another is called the van der Waals contact distance. This results from the electron clouds of two atoms unfavorably coming into contact. It can be shown that van der Waals forces are of the same origin as that of the Casimir effect, arising from quantum interactions with the zero-point field. The term "van der Waals forces" is also sometimes used loosely as a synonym for the totality of intermolecular forces. The term always includes the force between instantaneously induced dipoles (London dispersion force), sometimes includes the force between a permanent dipole and a corresponding induced dipole (Debye force), and – less frequently – includes the force between permanent dipoles (Keesom force).
The (complete) gamma function is defined to be an extension of the factorial to complex and real number arguments.
Debye toroidal moment of surface plasmons as SBIR ESCO model
Mann's Theorem
Awe Mann, are you Shur's Theorem?In discrete mathematics, Schur's theorem is any of several theorems of the mathematician Issai Schur. In differential geometry, Schur's theorem is a theorem of Axel Schur. In functional analysis, Schur's theorem is often called Schur's property, also due to Issai Schur.
In additive number theory, the Schnirelmann density of a sequence of numbers is a way to measure how "dense" the sequence is. (Insert dense joke here.) It is named after Russian mathematician Lev Schnirelmann, who was the first to study it: Schnirelmann density
There exists a positive integer such that every sufficiently large integer is the sum of at most primes. It follows that there exists a positive integer such that every integer is a sum of at most primes. The smallest proven value of is known as the Schnirelmann constant.
The universe (
In mathematics, a knot is defined as a closed, non-self-intersecting curve that is embedded in three dimensions and cannot be untangled to produce a simple loop (i.e., the unknot). While in common usage, knots can be tied in string and rope such that one or more strands are left open on either side of the knot, the mathematical theory of knots terms an object of this type a "braid" rather than a knot. To a mathematician, an object is a knot only if its free ends are attached in some way so that the resulting structure consists of a single looped strand. In topology, knot theory is the study of mathematical knots.
Definition of Gordian knot. 1 : an intricate problem especially : a problem insoluble in its own terms —often used in the phrase cut the Gordian knot. 2 : a knot tied by Gordius, king of Phrygia, held to be capable of being untied only by the future ruler of Asia, and cut by Alexander the Great with his sword. to cut the knot: to dispose of a difficulty summarily; to solve it by prompt, arbitrary action, rather than by skill or patience.
Cut the knot, An encyclopedic collection of math resources for all grades. Arithmetic games, problems, puzzles, and articles.
In mathematics (particularly calculus), an arbitrarily small positive quantity is commonly denoted ε; see (ε, δ)-definition of limit. In mathematics, Hilbert introduced epsilon terms
as an extension to first order logic; see epsilon calculus. In mathematics, the Levi-Civita symbol. In mathematics, to represent the dual numbers: a + bε, with ε2 = 0 and ε ≠ 0. In mathematics, sometimes used to denote the Heaviside step function. n set theory, the epsilon numbers are ordinal numbers that satisfy the fixed point ε = ωε. The first epsilon number, ε0, is the limit ordinal of the set {ω, ωω, ωωω, ...}.The conventional way to define the trig functions is to start with an acute angle
In the mathematical area of graph theory, a clique (/ˈkliːk/ or /ˈklɪk/) is a subset of vertices of an undirected graph such that every two distinct vertices in the clique are adjacent; that is, its induced subgraph is complete.
A clique in the social sciences, is a group of individuals who interact with one another and share similar interests.
Deriving Van der Waerden's theorem from Rado's theorem
Alpha (Α or α) and omega (Ω or ω) are the first and last letters of the Greek alphabet, and a title of Christ and God in the Book of Revelation. This pair of letters are used as Christian symbols, and are often combined with the Cross, Chi-rho, or other Christian symbols.
Omega male. noun [countable] a man who chooses not to have a powerful or important role in a social or professional situation. 'While the alpha male wants to dominate and the beta male just wants to get by, the omega male has either opted out or, if he used to try, given up.'
a mistaken belief, especially one based on unsound argument.
- Logica failure in reasoning which renders an argument invalid.
- faulty reasoning; misleading or unsound argument.
Gamma males typically represent the opposite of an alpha male. They certainly have alpha qualities, but they lack the self-confidence, direction, structure and identity that an alpha male has. They think they are bosses on the right track, but they are not.
Zeta male refers to the 4th social hierarchy position among males. (alpha - top, beta - second, omega - the rest). Zeta males consciously reject a the traditional social position as it is based on how they are valued by women.
Rado's theorem is a theorem from the branch of mathematics known as Ramsey theory. It is named for the German mathematician Richard Rado. It was proved in his thesis, Studien zur Kombinatorik.
'Hyperalarming' study shows massive insect loss
What is Geoengineering?
Climate geoengineering refers to large-scale schemes for intervention in
the earth’s oceans, soils and atmosphere with the aim of reducing the
effects of climate change, usually temporarily.
Consider:
What is Cantor dust?
George Cantor (1845-1918) constructed the Cantor dust. The curve is a base motif fractal which uses a square segment as base. The motif is to divide the square into nine equal parts and let only the outer four remain: The fractal dimension of the Cantor dust is equal to log4/log3, what is about 1.26186 1).
In set theory, Cantor's diagonal argument, also called the diagonalisation argument, the diagonal slash argument or the diagonal method, was published in 1891 by Georg Cantor as a mathematical proof that there are infinite sets which cannot be put into one-to-one correspondence with the infinite set of natural numbers. Such sets are now known as uncountable sets, and the size of infinite sets is now treated by the theory of cardinal numbers which Cantor began.
We’re altering the climate so severely that we’ll soon face apocalyptic consequences...
by Aylin Woodward
Scientists Promise to Create a Deflector Shield against Laser Weapons
Not Star Trek or Star Wars anymore.Researchers at defense giant BAE Systems calls the concept a Laser Developed Atmospheric Lens
(LDAL). The idea is to aim a powerful high-pulsed power laser system at
a section of Earth’s atmosphere, which will be temporarily ionized into
a sort of virtual mirror or lens.
Geologists rock weather warfare article 32 hearings
Consider:
D-21: A Mach 3 Drone
+
NUCLEAR SAVAGE The Islands of Secret Project 4.1
Correlate with proof.
The Brutality and Tenderness of Nick Cave’s Newsletters
Associate with:
Covalent networking the six flavors of quarks in the spirit of the French flag of Texas as a commodity fetish
The U.S. Agency for Global Media, formerly the Broadcasting
Board of Governors (BBG), is an independent agency of the United States
government. In 2010 Senator Tom Coburn had written an open letter to
then–Senate Minority Leader Mitch McConnell in August 2010 citing
"longstanding concerns regarding transparency and effectiveness of our
taxpayer funded international broadcasting agencies under the purview of
the Broadcasting Board of Governors."
These 6 Corporations Control 90% Of The Media In America
The U.S. Information and Educational Exchange Act of 1948, popularly
called the Smith–Mundt Act, is the basic legislative authorization for
propaganda activities conducted by the U.S. Department of State,
sometimes called "public diplomacy". Now, the Smith-Mundt Modernization Act of 2012 (part of the National Defense Authorization Act) has repealed the domestic prohibition, as 'Anti-Propaganda' Ban Repealed, Freeing State Dept. To Direct Its Broadcasting Arm At American Citizens
Dancing Italian Frogs and Toadies, Stooges v. Prescription Thugs, Olympic Gold
Gödel's Lost Letter and P=NP
“No one shall expel us from the paradise that Cantor has created for us.”
Cantor’s Non-Diagonal Proof
April 18, 2009
Opinion
Transparency Hasn’t Stopped Drug Companies From Corrupting Medical Research
The outrage over an influential doctor’s hidden millions is misplaced.
By Marcia Angell
Dr. Angell often writes on health policy and medical ethics.
Is that Cantor dust on your nose?
Number i versus number j for a piece of Pi in economics
What is Cantor dust?
George Cantor (1845-1918) constructed the Cantor dust. The curve is a base motif fractal which uses a square segment as base. The motif is to divide the square into nine equal parts and let only the outer four remain: The fractal dimension of the Cantor dust is equal to log4/log3, what is about 1.26186 1).
Cantor's Diagonal Argument
A Most Merry and Illustrated ExplanationIn set theory, Cantor's diagonal argument, also called the diagonalisation argument, the diagonal slash argument or the diagonal method, was published in 1891 by Georg Cantor as a mathematical proof that there are infinite sets which cannot be put into one-to-one correspondence with the infinite set of natural numbers. Such sets are now known as uncountable sets, and the size of infinite sets is now treated by the theory of cardinal numbers which Cantor began.
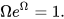
Comments
Post a Comment